Swift 5 SIMD (Single Instruction, Multiple Data) Vectors improvements
Swift 5 release improves SIMD vectors library
SIMD (Single Instruction, Multiple Data) allows to take advantage of hardware accelarated calculations for multiple application including vectors, equations, matrices, graphics.
SIMD framwork is part of Apple Swift standard library since iOS 9.
With recent release of Swift 5 Apple shipped much improved API working with SIMD. See Swift 5 Release Notes for Xcode 10.2
Now Swift 5 includes proposed SIMD Vectors support as part of standard library.
Usual C interface to simd makes it harder to use for developer, now with Swift 5 we can take advantage of generic protocol SIMD.
SIMD usage example
I’ve recently migrated my open source project Perspective Transform to take advantage of Swift 5 SIMD improvements.
Here is a block of code that takes advantage of matices multiplication and inverse. See Perspective.swift in the project:
private func calculateBasisVectorsToPointsMap() -> Matrix3x3 {
let baseVectors = Matrix3x3(Array(vectors[Vector3.indexSlice]))
let solution = baseVectors.inverse * vectors[Vector3.lastIndex + 1]
let scale = Matrix3x3(diagonal: solution)
let basisToPoints = baseVectors * scale
return basisToPoints
}
Without SIMD to make a similar calculations we had to spell out linear equation solution:
let a = -H*(x2a*x3a*y14 + x2a*x4a*y31 - x1a*x4a*y32 + x1a*x3a*y42)
let b = W*(x2a*x3a*y14 + x3a*x4a*y21 + x1a*x4a*y32 + x1a*x2a*y43)
let c = H*X*(x2a*x3a*y14 + x2a*x4a*y31 - x1a*x4a*y32 + x1a*x3a*y42) - H*W*x1a*(x4a*y32 - x3a*y42 + x2a*y43) - W*Y*(x2a*x3a*y14 + x3a*x4a*y21 + x1a*x4a*y32 + x1a*x2a*y43)
let d = H*(-x4a*y21*y3a + x2a*y1a*y43 - x1a*y2a*y43 - x3a*y1a*y4a + x3a*y2a*y4a)
let e = W*(x4a*y2a*y31 - x3a*y1a*y42 - x2a*y31*y4a + x1a*y3a*y42)
let f1 = (x4a*(Y*y2a*y31 + H*y1a*y32) - x3a*(H + Y)*y1a*y42 + H*x2a*y1a*y43 + x2a*Y*(y1a - y3a)*y4a + x1a*Y*y3a*(-y2a + y4a))
let f2 = x4a*y21*y3a - x2a*y1a*y43 + x3a*(y1a - y2a)*y4a + x1a*y2a*(-y3a + y4a)
let f = -(W*f1 - H*X*f2)
let g = H*(x3a*y21 - x4a*y21 + (-x1a + x2a)*y43)
let h = W*(-x2a*y31 + x4a*y31 + (x1a - x3a)*y42)
let temp = X * (-x3a*y21 + x4a*y21 + x1a*y43 - x2a*y43) + W * (-x3a*y2a + x4a*y2a + x2a*y3a - x4a*y3a - x2a*y4a + x3a*y4a)
var i = W * Y * (x2a*y31 - x4a*y31 - x1a*y42 + x3a*y42) + H * temp
see QuadrilateralCalc.swift for comparison.
SIMD advantages
Both solutions produce the same result, but SIMD code is much easier to understand, reason about and maintain. Plus with SIMD you can take advantage of hardware accelerated calculations as illustated here:

You can calculate upto 64 values at once for single operation, see [SIMD64
The above example solves the following matrix equation to find transformation:
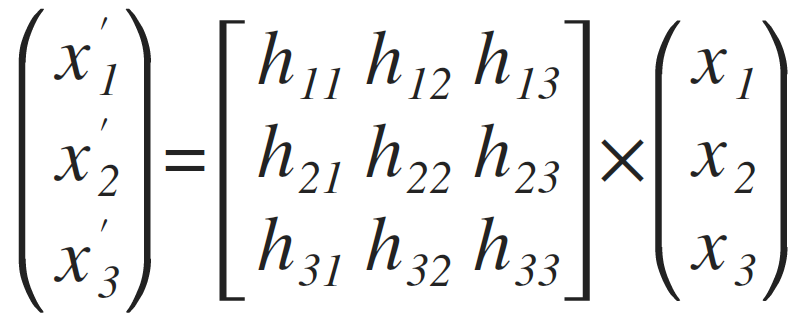
For more details on Perspective Transform Math see Matrix Math explained
Basis vectors space allows us to add extra dimention for our homogeneous coordinates:
SIMD calculations for animations
As a result we can now calculate perspective transformation matrix that can be applied to simulate 3D perspective for 2D graphics:
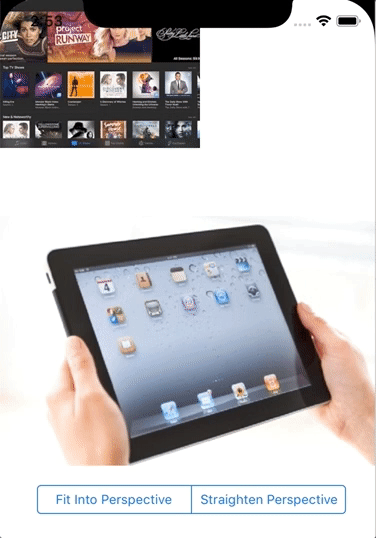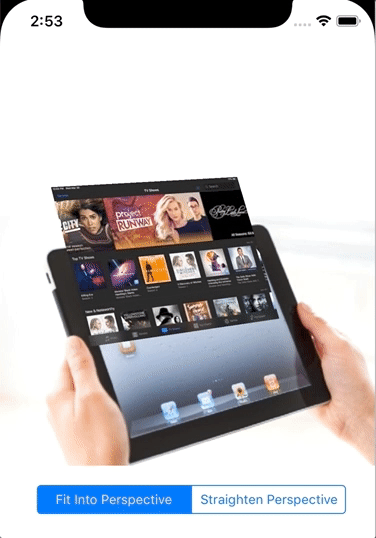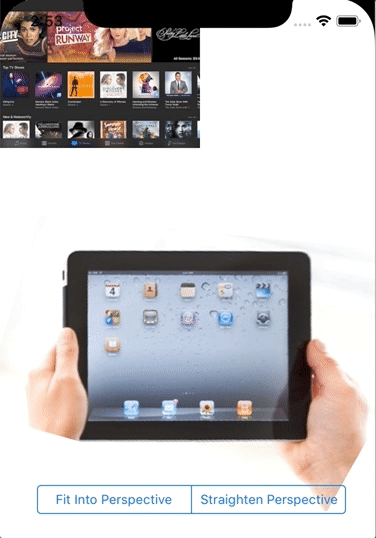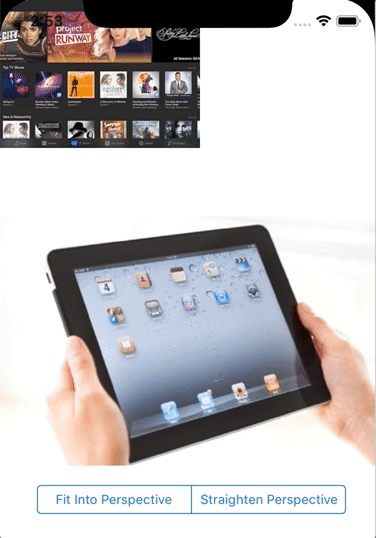
Next application of SIMD I am excited about is using cryprographical and pseudo random calculations for high performance shuffling of vector and matices data. How SIMD can benefit your Swift project?
